ইমিটার-স্থিতিশীল বিজেটি বায়াস সার্কিট

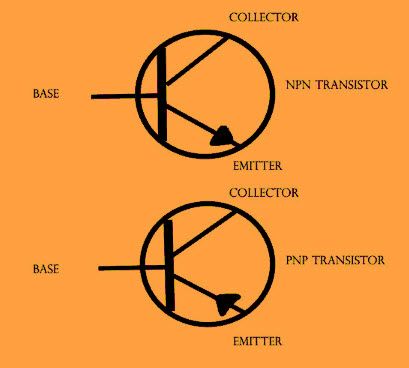
একটি কনফিগারেশন যাতে বাইপোলার জংশন ট্রানজিস্টর বা বিজেটি পরিবেষ্টিত তাপমাত্রার পরিবর্তনের সাথে সাথে তার স্থায়িত্ব বাড়ানোর জন্য একটি ইমিটার রোধকের সাথে জোরদার করা হয়, তাকে বিজেটি-র জন্য একটি ইমিটার স্থিতিশীল বায়াস সার্কিট বলা হয়।

আমরা ইতিমধ্যে কি তা অধ্যয়ন করেছি ট্রানজিস্টারে ডিসি বাইসিং , এখন আসুন এবং বিজেটি ডিসি বায়াস নেটওয়ার্কের স্থিতিশীলতার উন্নতির জন্য একটি ইমিটার রোধকারী কীভাবে ব্যবহার করা যেতে পারে তা শিখি।

ইমিটার স্থিতিশীল বায়াস সার্কিট প্রয়োগ করা

বিজেটি-র ডিসি বায়াসে ইমিটার রেজিস্টরের অন্তর্ভুক্তি উচ্চতর স্থায়িত্ব দেয়, অর্থাত্ ডিসি বায়াস স্রোত এবং ভোল্টেজগুলি আরও বেশি কাছাকাছি থাকতে থাকে যেখানে তারা বাহ্যিক পরামিতিগুলি বিবেচনা করে সার্কিট দ্বারা স্থির করা হয়েছিল যেমন তাপমাত্রার বিভিন্নতা, এবং ট্রানজিস্টর বিটা (লাভ),

নীচের প্রদত্ত চিত্রটি বিজেটির বিদ্যমান স্থির পক্ষপাতী কনফিগারেশনটিতে ইমিটার-স্ট্যাবিলাইজড বায়িংিং কার্যকর করার জন্য একটি ইমমিটার রোধকারী একটি ট্রানজিস্টর ডিসি বায়াস নেটওয়ার্ক দেখায়।

চিত্র 4.17 বিএমটি বায়াস সার্কিট ইমিটার রোধকের সাথে

আমাদের আলোচনায় আমরা প্রথমে সার্কিটের বেস-এমিটার অঞ্চলটির চারপাশে লুপটি পর্যবেক্ষণ করে নকশার বিশ্লেষণ শুরু করব এবং তারপরে সার্কিটের কালেক্টর-ইমিটারের পাশের লুপটি আরও তদন্তের জন্য ফলাফলগুলি ব্যবহার করব।

বেস-ইমিটার লুপ

আমরা উপরের বেস-ইমিটার লুপটি চিত্র 4.18 তে নীচে দেখানো পদ্ধতিতে পুনরায় আঁকতে পারি এবং যদি আমরা প্রয়োগ করি কির্ফোফের ভোল্টেজ আইন ঘড়ির কাঁটার দিকের এই লুপটিতে, নীচের সমীকরণটি পেতে আমাদের সহায়তা করে:

+ ভিসি = আইবিআরবি - ভিবিই - আইইআরই = 0 ------- (4.15)

আমাদের পূর্ববর্তী আলোচনা থেকে আমরা জানি যে: আইই = (β + 1) খ ------- (4.16)

আইকিউ এর মান প্রতিস্থাপনের জন্য (4.15) নিম্নলিখিত ফলাফল সরবরাহ করে:

ভিসিসি = আইবিআরবি - ভিবিই - (β + 1) আইবিআরআই = 0

তাদের নিজ নিজ গোষ্ঠীতে শর্তাদি রাখলে নিম্নলিখিত ফল পাওয়া যায়:

আপনি যদি আমাদের পূর্ববর্তী অধ্যায়গুলি থেকে স্মরণ করেন তবে স্থির পক্ষপাত সমীকরণটি নিম্নলিখিত আকারে উত্পন্ন হয়েছিল:

যদি আমরা এই স্থির পক্ষপাত সমীকরণকে (4.17) সমীকরণের সাথে তুলনা করি তবে আমরা বর্তমান আইবি-র জন্য দুটি সমীকরণের মধ্যে পার্থক্যটিই খুঁজে পাই শব্দটি (β + 1) আরই।

যখন সিরিজ ভিত্তিক কনফিগারেশন আঁকার জন্য 4..১17 সমীকরণটি ব্যবহৃত হয় তখন আমরা একটি আকর্ষণীয় ফলাফল বের করতে সক্ষম হয়ে থাকি, যা প্রকৃতপক্ষে সমীকরণ ৪.১17 এর মতো।

চিত্র 4.19-তে নিম্নলিখিত নেটওয়ার্কের উদাহরণ নিন:

যদি আমরা বর্তমান আইবি-র জন্য সিস্টেমটি সমাধান করি, তবে এক্কে প্রাপ্ত একই সমীকরণের ফলাফল। 4.17। লক্ষ্য করুন যে বেস থেকে ইমিটার ভিবিইতে ভোল্টেজের পাশাপাশি, রেজিস্টর আরই আবার একটি স্তর দ্বারা বেস সার্কিটের ইনপুটটিতে উপস্থিত হতে দেখা যায় (β + 1)।

অর্থ, ইমিটার রোধকারী যা সংগ্রাহক-ইমিটার লুপের একটি অংশ গঠন করে তা প্রদর্শিত হয় (β + 1) আরই বেস-ইমিটার লুপে

ধরে নিই যে বেশিরভাগ বিজেটি-র ক্ষেত্রে β প্রায় 50 এর উপরে হতে পারে, ট্রানজিস্টারের প্রেরকগুলিতে প্রতিরোধক বেস সার্কিটে উল্লেখযোগ্যভাবে বড় হতে পারে। অতএব, আমরা চিত্র 4.20 এর জন্য নিম্নলিখিত সাধারণ সমীকরণ অর্জন করতে সক্ষম হয়েছি:

রি = (β + 1) আরই ------ (4.18)

ভবিষ্যতের অনেকগুলি নেটওয়ার্ক সমাধান করার সময় আপনি এই সমীকরণটি বেশ কার্যকর পাবেন। প্রকৃতপক্ষে, এই সমীকরণটি একটি সহজ উপায়ে 4.17 স্মৃতিস্তম্ভকে সহজ করে দেয়।

ওহমের আইন অনুসারে আমরা জানি যে কোনও নেটওয়ার্কের মাধ্যমে কারেন্টটি সার্কিটের প্রতিরোধের দ্বারা বিভক্ত ভোল্টেজ।
বেস-ইমিটার ডিজাইনের ভোল্টেজ = = ভিসি - ভিবিই

৪.১17-এ দেখা প্রতিরোধগুলি হ'ল আরবি + আরইআর , যা প্রতিফলিত হয় (β + 1), এবং ফলাফল যা আমরা EQ 4.17 এ পেয়েছি।

সংগ্রাহক mit ইমিটার লুপ

উপরের চিত্রটি সংগ্রহকারী-এমিটার লুপটি প্রয়োগ করে দেখায় কির্ফোফের আইন ঘড়ির কাঁটার দিকে নির্দেশিত লুপটিতে আমরা নীচের সমীকরণটি পাই:

+ YESTERDAY + তুমি + আইসিআরসি - ভিসিসি = 0

নীচে দেওয়া হিসাবে নির্গত স্থিতিশীল পক্ষপাত সার্কিটের জন্য ব্যবহারিক উদাহরণ সমাধান করা:



উপরের চিত্র 4.22 তে যেমন ইমিটার বায়াস নেটওয়ার্ক রয়েছে তার জন্য নিম্নলিখিতটি মূল্যায়ন করুন:

1. আইবি
2. আইসি
3. তুমি
4. উ
5. এবং
6. ইটিসি
7. ভিবিসি

স্যাচুরেশন স্তর নির্ধারণ করা হচ্ছে

সর্বাধিক সংগ্রাহক বর্তমান যা সংগ্রাহক হয় স্যাচুরেশন স্তর একটি ইমিটার পক্ষপাতমূলক নেটওয়ার্কের জন্য আমাদের আগের জন্য প্রয়োগ করা হয়েছিল একই কৌশলটি নিয়োগ করে গণনা করা যেতে পারে স্থির পক্ষপাত সার্কিট ।

এটি উপরের চিত্রের 4.23 হিসাবে উল্লিখিত বিজেটি-র সংগ্রহকারী এবং ইমিটার লিডস জুড়ে একটি শর্ট সার্কিট তৈরি করে প্রয়োগ করা যেতে পারে এবং তারপরে আমরা নিম্নলিখিত সূত্রটি ব্যবহার করে ফলাফল সংগ্রহকারী বর্তমানকে মূল্যায়ন করতে পারি:

ইমিটার স্থিতিশীল বিজেটি সার্কিটে স্যাচুরেশন কারেন্ট সমাধানের সমস্যা উদাহরণ:

লোড লাইন বিশ্লেষণ

ইমিটার-বায়াস বিজেটি সার্কিটের লোড-লাইন বিশ্লেষণটি আমাদের আগের আলোচিত স্থির-পক্ষপাত কনফিগারেশনের সাথে বেশ মিল।

আইবি স্তর হিসাবে কেবলমাত্র পার্থক্য [যেমনটি আমাদের একা (৪.১17) থেকে প্রাপ্ত) নীচের চিত্র ৪.২৪ (আইবিকিউ হিসাবে চিহ্নিত) হিসাবে বর্ণিত বৈশিষ্ট্যের উপর আইবি স্তরকে সংজ্ঞায়িত করে।